Поступило в редакцию: Июль 2021
УДК 544.23.022.346
Fluorine Notes, 2021, 137, 5-6
СВОЙСТВА МОЛЕКУЛ ПЕРФТОРИРОВАННОГО СВЕРХРАЗВЕТВЛЕННОГО ПОЛИФЕНИЛЕНГЕРМАНА
В. В. Волков1, О. Г. Замышляева2, А. Г. Иванова1, М. С. Китай3, А. А. Сафонов4.
1Институт Кристаллографии им. А.В.Шубникова ФНИЦ «Кристаллография и фотоника» РАН, Россия, Москва
2ФГАОУ ВО Национальный исследовательский Нижегородский государственный университет им. Н.И. Лобачевского, химический факультет, Россия, Нижний Новгород
3Институт Фотонных Технологий ФНИЦ «Кристаллография и фотоника» РАН, Россия, Москва, mkitai@mail.ru
4Центр Фотохимии ФНИЦ «Кристаллография и фотоника» РАН, Россия, Москва
Аннотация: Рассмотрена простейшая структура перфторированного полимера сверхразветвленного полифениленгермана (СРП ПФГ). Для этой структуры рассчитаны характерные размеры и молекулярные массы полимеров первого - третьего поколений. Проведены эксперименты по мало-угловому рентгеновскому рассеянию (МУРР) и рентгеновской дифракции СРП ПФГ. Исходя из полученных экспериментальных данных, определены отдельные характерные размеры аморфных полимерных макромолекул.
Ключевые слова: Характерные размеры молекулы перфторированного сверхразветвленного полифенилгермана.
Введение
В современном мире полимеры – это одни из основных материалов, используемых в самых различных отраслях. В большинстве случаев полимеры состоят из линейных макромолекул, которые имеют форму отдельных длинных цепей. При этом каждая отдельная макромолекула в процессе полимеризации имеет одну точку роста, в которой мономеры последовательно соединяются между собой ковалентными связями.
Полимеризация бис- три- и поли- функциональных соединений приводит к образованию разветвленных полимеров, для которых количество точек роста в макромолекуле увеличивается в процессе полимеризации. Параметры, характеризующие различные полимеры, обладают многоуровневой структурой (химической, топологической, надмолекулярной). Это относится и к сверхразветвленным полимерам (СРП), исследуемым в настоящей работе, синтез и описание основных свойств СРП рассмотрен в [1].
СРП – это полимеры сложной архитектуры, отличающиеся топологией макромолекул, высокой объёмной концентрацией звеньев цепи внутри макромолекул и наличием большого числа функциональных групп на их периферии. Одно из основных достоинств синтеза СРП, используемого в [1], (по сравнению с традиционными процессами полимеризации), - это высокая скорость одностадийных методов полимеризации.
Среди органических полимеров значительный интерес вызывают фторсодержащие полимеры. Перфторированные (т.е. содержащие максимально возможный процент фтора F) полимеры обладают малой величиной диэлектрического поглощения (вплоть до низкочастотной части ТГц диапазона), сравнительно малым значением коэффициента рефракции, обладают механической прочностью, высокой термостойкостью и химической устойчивостью [2]. Актуальными для таких полимеров являются их поверхностные свойства. У них низкая величина поверхностной энергии, что внешне проявляется, как малый коэффициент механического трения с поверхностью полимера. Отметим, что, полимеризация некоторых из таких полимеров (и сополимеров) требует сверхвысоких давлений, что затрудняет их синтез.
Постановка задачи и методы её решения
В настоящей работе исследовались молекулы аморфного перфторированного сверхразветвленного полифениленгермана (СРП ПФГ). Первый целенаправленный синтез такого полимера одностадийным методом был осуществлен сотрудниками школы академика Г.А.Разуваева, когда в качестве мономеров Флори типа АВ3 применялись производные германия (C6F5)3GeX, (причём обычно использовался X=H [3]). При полимеризации соединения, исследованного в настоящей работе, исходным мономером был трис-(пентафторфенилен)герман. Он в течении часа реагировал (при комнатной температуре) с триэтиламином (H3C-CH2)3N. Описание реакции полимеризации СРП ПФГ в этом случае см. в [1].
Теоретические расчётные исследования молекул полимера были проведены в предположении, что молекулы имеют некую определённую регулярную структуру (такую, как на Рис. 1). Для такой структуры СРП ПФГ квантово-химические расчеты молекулы были проведены с помощью программы ORCA [4]. При расчётах использовалась процедура HF-3c [5], основанная на методе Хартри-Фока с тремя поправками (дисперсионной, на неполноту используемого базиса и на базисную суперпозиционную ошибку). Процедура HF-3c – это готовая процедура, включенная в программу ORCA.
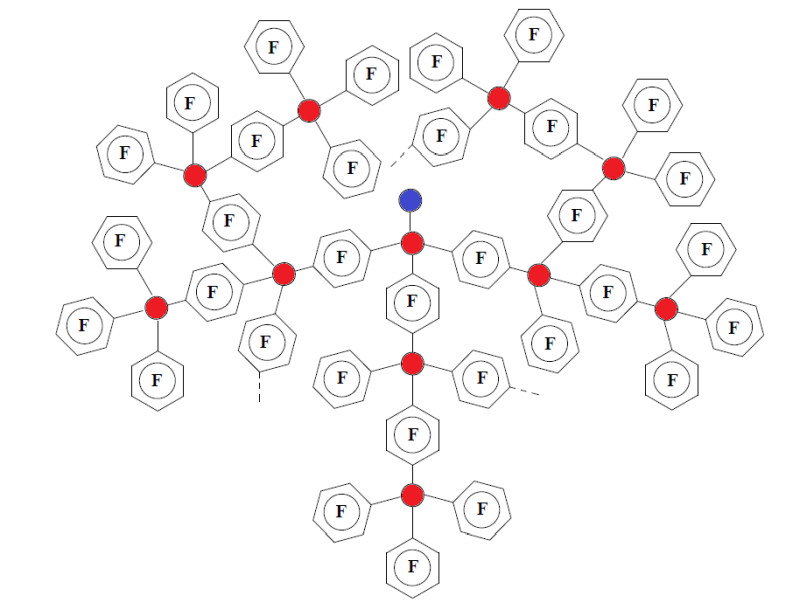
Рисунок 1. Модель упрощенной структуры полимера СРП ПФГ [1, c.34].
На рисунке красным заштрихованы атомы германия (Ge) и синим атом водорода (Н) в центре структуры.
Рентгеновские измерения рассеяния и дифракции были проведены на образцах СРП ПФГ в виде мелкодисперсного порошка. В этих экспериментах использовался порошок СРП ПФГ третьего поколения.
Измерения интенсивности малоуглового рентгеновского рассеяния (МУРР) проводили на дифрактометрах АМУР-К и “HECUS SYSTEM-3", оснащенных коллимационными системами Кратки, и однокоординатными позиционно-чувствительными детекторами ОД3М, при фиксированной длине волны излучения = 1.542 Å (CuKa линия острофокусной трубки с медным анодом, монохроматор из пиролитического графита). Сечение рентгеновского пучка составляло 0.2 х 8 мм, область углов рассеяния соответствовала диапазону значений модуля вектора рассеяния 0.01 < s < 1.15 Å-1 (s = (4π•sinθ)/λ, 2 - угол рассеяния). Образцы помещали в стеклянную кювету. Рентгеновская дифрактограмма образца измерялась в геометрии Брэгга-Брентано [6] («на отражение») на дифрактометре Rigaku MiniFlex 600 (CuKα-излучение, λ= 1.5418Å, 40кВ, 15мА, Ni-Kβ-фильтр) в угловом диапазоне 2θ = 4 - 45º, с шагом сканирования 0.02º и скоростью 0.8º/мин. Размер пучка, падающего на образец, задавался горизонтальной и вертикальной щелями - 10 мм и 0.625º соответственно из лавсановой пленки толщиной 10 мкм. Время измерений одного образца составляло 20 минут. Экспериментальные данные были нормированы на интенсивность падающего пучка, после чего в них вводилась поправка на коллимационные искажения. Из данных рассеяния образцами вычитали рассеяние от пустой кюветы.
Для исследований методом рентгеновской дифракции порошок СРП ПФГ наносился на стеклянную кювету. Рентгеновская дифрактограмма образца измерялась в геометрии Брэгга-Брентано [6] («на отражение») на дифрактометре Rigaku MiniFlex 600 (CuKα-излучение, λ= 1.5418Å, 40кВ, 15мА, Ni-Kβ-фильтр) в угловом диапазоне 2θ = 4 - 45º, с шагом сканирования 0.02º и скоростью 0.8º/мин. Размер пучка, падающего на образец, задавался горизонтальной и вертикальной щелями - 10 мм и 0.625º соответственно.
Размеры молекул СРП ПФГ
Исходным мономером является молекула три(пентафторфенил)германа, изображенная рис.2.
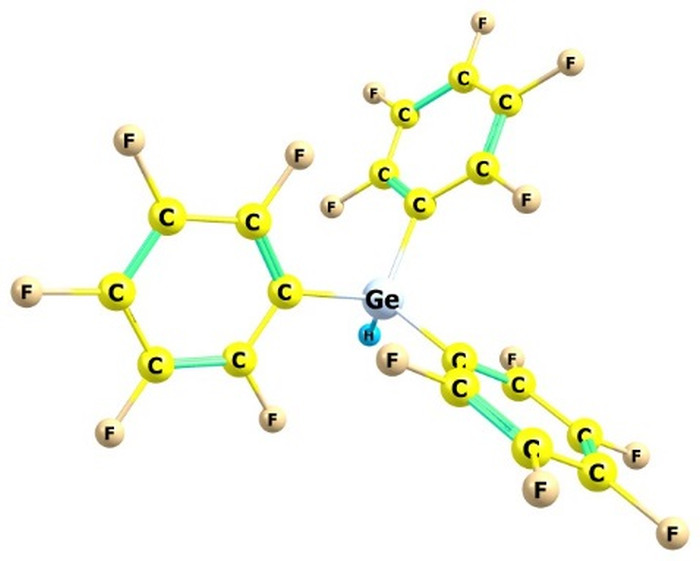
Рисунок 2. Молекула мономера три(пентафторфенил германа) (F15C18)GeH.
В центре мономера находится атом Ge, ковалентно связанный с атомом водорода Н. Полимер формируется путем присоединения мономеров по атомам F в пара-положениях всех фенильных групп. В случае бесконечного (большого) полимера, в качестве центра можно рассматривать любой атом Ge, и все такие атомы (кроме одного) имеют четыре присоединенные фенильные группы. Далее рассматривались молекулы, полученные добавлением мономеров к тетра(пентафторфенил)герману, т.е. молекулы следующей (второй) стадии. Для неё была оптимизирована геометрия и рассчитаны колебательные частоты: они начитаются с 5 см–1, диаметр молекулы около 16Å.
На следующем третьем этапе имеется двенадцать позиций для присоединения, результатом является молекула, состоящая из 573 атомов. Для нее также оптимизирована геометрия и можно посчитать колебательные частоты. В рамках упрощенной структуры полимера (см. Рис. 1) дальнейшее присоедините мономеров по всем доступным позициям невозможно по стерическим причинам.
В Таблице 1 показаны результаты расчетов молекулярной массы макромолекулы СРП ПФГ в зависимости от номера поколения, а также их характерные размеры. Для второго поколения форма молекулы близка к сферической (диаметром d), для третьего поколения – форма близка к эллипсоиду
Таблица 1. Результаты расчетов молекулярной массы макромолекулы СРП ПФГ.
|
No поколения СРП ПФГ |
Масса макромолекулы MW, а.е.м. |
Характерные размеры молекулы, А0 |
|
1 |
575 |
|
|
2 |
2239 |
d≈16 |
|
3 |
7232 |
≈30 x 30 x 19 |
Рассчитанная молекулярная масса MW для третьего поколения СРП ПФГ (7232 а.е.м.) соответствует интервалу, в котором была измерена масса низкомолекулярной фракции для этих полимеров [3, c.49]. Авторы также объясняют ограниченность MW стерическими затруднениями, возникающими при полимеризации СРП ПФГ. Показано, что MW фактически ограничена величиной 22 000 а.е.м. для любых моделей третьего поколения СРП ПФГ [3, c.49]. По сравнению с данными Таблицы 1, наблюдается трехкратное различие, что, на наш взгляд, обусловлено ограниченностью расчетной модели.
Мaлоугловое paссеяние pентгеновских лучей (МУРР) и нейтpонов является одним из нaиболее эффективных неразрушающих методов изучения нaдaтомной стpуктуpы неупорядоченных и частично упорядоченных материалов пpи paзpешении 1–100 нм (т.н. область наноразмеров). Глaвным достоинством методa малоуглового рассеяния является его универсальность: он может быть использовaн при исследовaнии неупоpядоченных объектов, и не тpебует специaльной подготовки обpaзцов. Экспериментальные результаты МУРР, полученные для СРП ПФГ отражены на Рис. 3.
Данные МУРР, зарегистрированные при s вблизи 0.9 (A0)-1 показывают очень слабовыраженный максимум, соответствующий характерному размеру d = 2π/0,9 7A0. Этот максимум, согласно [8, c.78], отражает внутреннее строение молекулы с разрешением порядка 1 нм. Теоретические расчеты, проведённые для второго поколения ПФГ, дают очень близкие данные, d 6,6 A0 расстояние между различными атомами Ge, находящимися с противоположных сторон от одного и того же фтор-фенильногое кольца.
Форма кривой интенсивности МУРР подтверждает данные СРП ПФГ - это аморфное вещество, так как на кривой рассеяния отсутствуют выраженные дифракционные максимумы.
С помощью приближения Гинье [9] по начальному участку кривой рассеяния можно оценить радиус инерции часиц Rg:
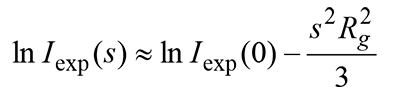 (1)
(1)
Это приближение основано на модели, предполагающей, что вещество состоит из одинаковых частиц. Тем не менее, в случае полидисперсных образцов, анализ формы графика интесивности МУРР позволяет оценить распределение молекулярных частиц и их агрегатов по радиусам инерции с помощью метода касательных [10], которые проводят на разных участках кривой рассеяния, построенной в координатах Гинье. Этот метод, нередко используемый многими исследователями, является приближенным, но он позволяет грубо оценить распределение рассеивающих неоднородностей по размерам [10]. Заметим, что приближение Гинье используют в узких пределах модуля вектора рассеяния, а касательные на графике Гинье отражают размерные параметры в узких пределах модуля вектора рассеяния. Для проведенных измерений МУРР, вместо касательных использовали линейную аппроксимацию данных Гинье на интервалах шириной около 5% от полного диапазона, т.е. осуществляли статистическое усреднение результатов по ближайшей окрестности. Следует отметить, что в аппроксимации Гинье параметр формфактора молекулы не применяется.
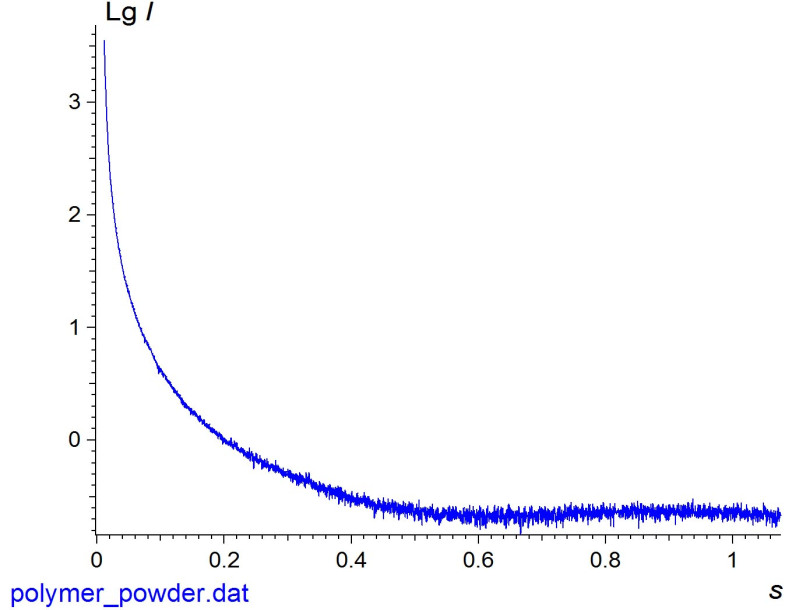
Рисунок 3. Экспериментальная интенсивность малоуглового рассеяния I от образца порошка СРП ПФГ.
Основной результат (по концентрации молекул) приходится на s > 0.2 (A0)-1 . Из Рис. 4 следует, что граница между двумя участками на кривой МУРР соответствует точке с минимумом радиуса кривизны . Согласно[12] радиус кривизны плоской кривой y=y(x) вычисляется по формуле:
(1/ρ) = y’’/ [1+(y’)2]3/2 (2)
где y’= dy /dx – первая производная; y’’ = d2y / dx2 – вторая производная от функции y=y(x). Горизонтальная линия на Рис. 4 показывает примерное положение точки с минимумом радиуса кривизны. Малоугловая часть соответствует рассеянию на хаотических флуктуациях плотности агрегатов молекул, при больших углах основной вклад в рассеяние дает форма молекул и, по мере увеличения угла, их внутренняя структура.
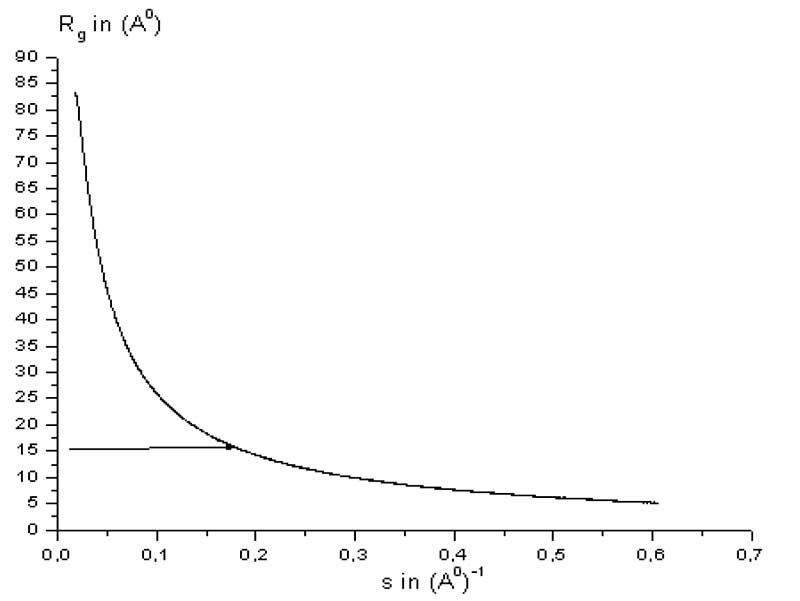
Рисунок 4. Зависимость радиуса инерции Rg от модуля вектора рассеяния.
Результаты измерений рентгеновской дифракции для порошка СРП ПФГ приведены на Рис. 5.
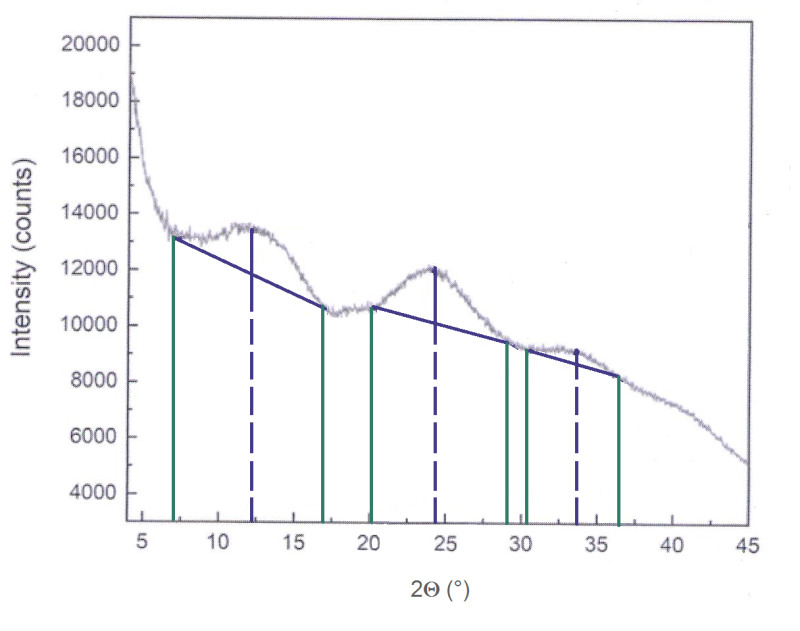
Рисунок 5. Экспериментальные результаты дифрактограммы СРП ПФГ.
Общий характер кривой Рис. 5 подтверждает, что ПФГ – это аморфное вещество, которое имеет три характерных размера. Углы, соответствующие максимумам 2 равны: 120, 240 и 33,30. В работе [13] приводится т.н. формула Шерера, по которой велся расчёт характерных размеров неоднородности L.
Характерный размер неоднородности
L=λ /β• ( cosθ ) (3)
здесь - полуширина максимума в радианах. Величина характеризует отношение максимумов в дифрактограмме к полному уровню сигнала для данного угла. Чем больше величина , тем заметнее на общем фоне сигнал.
Таблица 2. Характерные размеры молекул СРП ПФГ.
|
No п/п |
2θ,max, Град. |
Cosθ |
Δ(2θ), Град. |
Δθ, Град. |
β, Радиан |
L, A0 |
α |
|
1 |
12 |
0,995 |
9,67 |
4,84 |
0,084 |
18,5 |
0,18 |
|
2 |
24 |
0,978 |
8,33 |
4,16 |
0,073 |
21,6 |
0,23 |
|
2 |
33,3 |
0,958 |
5,0 |
2,50 |
0,044 |
36,6 |
0,12 |
Использование молекул СРП ПФГ
Особенности молекул СРП ПФГ связаны с тем, что эти молекулы легко растворяются в большинстве растворителей, а сами молекулы являются нетоксичными [1]. Для «раздувания» (получения большого объёма внешне доступных пор) в полимере возможно использование сверхкритического СО2 в процессе порообразования [14]. Это может позволить в дальнейшем использовать СРП ПФГ в качестве матрицы для введения необходимых лекарств.
Как и большинство перфторированных полимеров, СРП ПФГ может быть использован в качестве материала (или его составляющей) в микроэлектронике.
Благодарности
Работа была выполнена при поддержке Министерства науки и высшего образования РФ. Рентгено-дифракционный анализ осуществлен с использованием оборудования Центра Коллективного Пользования ФНИЦ «Кристаллография и фотоника» РАН. Авторы статьи благодарят А.П.Свиридова и В.И.Соколова за полезные обсуждения.
Список литературы
- О. Г. Замышляева, (Со)полимеры различной архитектуры на основе перфторированных гидридов германия: синтез, структура и свойства, дисс. … доктора хим. наук, НГУ, Нижний Новгород, 2013.
- М. С. Китай, В. В. Волков, А. А. Жаров, Я. В. Зубавичус, П. В. Конарев, М. М. Назаров, Е. В. Полунин, Ю. Е. Погодина, В. И. Соколов, Оптические свойства аморфных перфторированных полимеров в терагерцовом диапазоне частот, Журн. прикл. спектр., 2018, 85(3), 364-371.
- М. Н. Бочкарев, В. Б. Силкин, Л. П. Майорова, Г. А. Разуваев, Ю. Д. Семчиков, В. И. Шерстяных, Полифениленгерман – полимерный материал нового типа; Металлорганическая химия, 1988, 1(1), 196-200.
- F. Neese, The ORCA program system, Wiley, Rev.: Comput. Mol. Sci., 2017, 2, 73-78.
- Sure, R.; Grimme, S., Corrected small basis set Hartree-Fock method for large systems, J. Comput. Chem., 2013, 34, 1672-1685.
- J. Brentano, Focusing method of crystal powder analysis by X-rays; Proc. Phys. Soc., London, 1924, 37(1), 184-193.
- М. А. Симонова, Структурно-конформационные свойства сверхразветвленных перфторированных полифениленгерманов и их линейно-дендритных структур с полистиролом и полиметилметакрилатом, дисс. …канд. физ.-мат. наук, ИВС РАН, Санкт-Петербург, 2014.
- Э. В. Штыкова, Метод малоуглового рентгеновского рассеяния в структурной диагностике надмолекулярных комплексов, дисс. … доктора хим. наук, Институт кристаллографии РАН, Москва, 2015.
- Д. И. Свергун, Л. А. Фейгин, Рентгеновское и нейтронное малоугловое рассеяние, Москва, Наука, 1986, 280с.
- А. И. Китайгородский, Рентгеноструктурный анализ мелкокристаллических и аморфных тел, Москва, Гостехидат, 1952.
- A. V. Smirnov, V. Yu. Kalyakin, B. A. Fedorov, Assessment for applicability of the “tangent technique” in X-ray small-angle scattering, Nanosystems: Physics, Chemistry, Mathematics, 2016, 7(6), 1002-1009.
- Г. Корн, Т. Корн, Справочник по математике, 1975, 519с.
- М. С. Китай, М. М. Назаров, Д. А. Сапожников, В. И. Быков, М. В. Бермешев, С. А. Булгакова, Б. Ф. Шклярук, Структурно-чувствительные максимумы в спектрах поглощения полимеров в терагерцовой области частот, Известия ВУЗов «Радиофизика», 2014, LVII(12), 984.
- Е. С. Алексеев, А. Ю. Алентьев и др., Сверхкритические флюиды в химии, Успехи химии, 2020, 89(12).
Статья рекомендована к публикации к.х.н. В.Л. Дон
Fluorine Notes, 2021, 137, 5-6